※ 논문을 필자가 이해한 대로 정리한 내용이니 내용적 오류가 있는 부분은 댓글로 남겨주기 바랍니다!
Abstract
신경망의 깊이는 모델의 성능개선에 있어 핵심적으로 중요한 요소이다. 하지만 신경망이 깊어질수록 모델은 더 복잡해지고 기울기 소실, degradation, overfitting 등으로 인한 성능저하를 야기할 수 있다는 문제점이 있다. 본 논문에서는 residual learning framework을 통해 이 문제를 개선하였음을 제시한다. residual learning의 핵심은 해당 층의 입력값으로 활용되는 이전 층의 결과값을 학습에 활용하는 것이다. 이러한 방법을 사용한 ResNet은 단순히 층을 깊게 쌓아올린 VGG 방식보다 ImageNet dataset에 있어 오차를 3.57% 더 줄일 수 있었다. residual learning은 단순히 classification 뿐만 아니라 localization, object detection, segmentation에서도 성능 개선을 보였다.
1. Introduction
심층 신경망에서 "깊이"는 매우 중요한 요소이다. 더욱 높은 수준의 특성을 추출하여 더 복잡한 문제를 해결해 줄 수 있기 때문이다.
Is learning better networks as easy as stacking more layers?
하지만 층을 깊이 쌓는 것은 쉬운 반면 그러한 신경망을 학습시키는 것은 별개의 문제였다. 깊은 층을 가진 인공신경망을 학습시키는데 발생하는 악명높은 문제들이 있었기 때문이다. 대표적으로 vanishing/exploding gradient 문제는 네트워크의 값의 수렴을 방해하는 문제를 야기했지만 가중치 초기화(Initialization), 정규화 층(Normalization layer)의 도입으로 해결되었다.

값이 수렴하기 시작하자 이제는 degradation 문제가 나타났다. 이는 네트워크가 깊어질수록 성능이 저하되는 문제였다. 위 사진을 보면 56개의 층을 가진 네트워크가 26개의 층을 가진 것보다 에러가 더 높게 나타는 것을 알 수 있다. 이 현상은 overfitting 문제는 아니었다. 보다시피 training error조차 깊은 층에서 더 높았기 때문이다.
한가지 해결책은 깊은 층에서는 identity mapping을 적용하는 것이었다. 얕은 층의 모델의 구조를 그대로 가져오되 identity mapping이 적용된 층들을 더 추가하는 것이다. 즉 깊은 층에서는 입력값(input)을 그대로 출력값(output)으로 내보내는 구조인데 이는 얕은 층의 모델보다 성능이 더 낮아지는 경우는 없어야 한다는 것을 나타낸다. 얕은 층 모델의 마지막 층을 통과하여 나온 값이 깊은 층 모델의 마지막 층까지 그대로 유지되기 때문이다. 이러한 발상에서 조금 더 나아간 것이 deep residual learning framework이다.
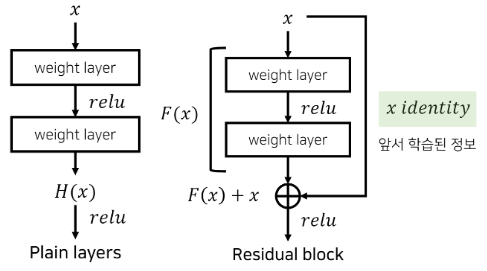
residual mapping + identity shortcut connection → degradation 해결
Underlying mapping(=original mapping)을 H(x)라 하자. H(x)는 모든 층들을 통과해 나온 값이다. 이때 추가된 층만을 F(x)라고 정의한다면 F(x) = H(x) - x가 된다. 이러한 F(x)는 해당 층을 지날 때 값이 얼마나 변동했는지 설명해 줄 수 있다. 다르게 말하면 "잔차 값"을 나타낸다고 할 수 있는 것이다. 따라서 H(x) - x로 정의된 F(x)를 잔차함수(residual function)라고 하며 F(x) = H(x) - x이와 같이 정의된 mapping을 residual mapping 이라고 한다. 각 layer에서는 H(x)에 근사하도록 학습하므로 original mapping이 H(x) = F(x) + x로 재구성된다. 기존의 original mapping은 H(x) = F(x)를, residual mapping은 H(x) = F(x) + x를 학습하는 것이다. 이때 H(x)에 대한 optimal solution이 identity mapping이라고 하면 residual mapping이 학습하기 훨씬 쉽게 된다. H(x) = F(x) = x (original mapping)에서는 F(x) = x가 되도록 하는 F(x)의 가중치들을 일일이 구해야 하지만 H(x) = F(x) + x = x (residual mapping)에서는 F(x)를 0으로 만들면 되기 때문이다.
residual mapping과 identity mapping은 shortcut connection을 통해 구현되는데 이는 하나 이상의 층을 건너뛰게 만드는 방식이다. 위 그림을 보면 입력값으로 활용되는 x가 weight layer를 건너뛰고 F(x)에 따로 더해지고 identity mapping에도 활용이 된다. F(x) + x = x의 식에서 x는 shortcut connection을 통해서 전달된 값인 것이다. 이러한 identity shortcut connection은 추가적인 파라미터나 복잡한 계산을 필요로 하지 않고 아주 간단히 구현이 된다!
3. Deep Residual Learning
3.1 Residual Learning
Underlying mapping을 추가된 층을 최적화시키기 위한 목적함수인 H(x)라 하자. 다중 비선형 층이 복잡한 함수를 점근적으로 근사할 수 있다면 잔차함수인 H(x) - x도 점근적으로 근사시키는 것이 가능하다. 애초에 H(x)가 다중 비선형 층이기 때문에 H(x)에서 x만큼을 빼준 잔차함수도 근사가 가능하다는 것은 당연하다. 잔차함수의 형태는 F(x) = H(x) - x이고, 목적함수가 H(x)이기 때문에 최적화는 H(x)를 기준으로 진행된다. 따라서 mapping은 H(x) = F(x) + x로 새로 정의되고 여기에 optimal solution인 identity mapping을 적용하면 F(x) + x = x를 최적화시키는 문제가 되는 것이다. 새로 정의되기 이전의 mapping에서는 다중 비선형 층인 F(x)가 x의 값을 갖도록 가중치들을 직접 구해야하기 때문에 어려운 부분이 있었다. 하지만 새로 정의된 mapping에서는 F(x)를 0으로만 만들어주면 된다. 따라서 더 쉽게 학습이 가능한 것이다. 그렇다면 여기서 의문점이 한 가지 있다.
identity mapping이 optimal solution이라고 어떻게 보장할 수 있는가?
실제로는 identity mapping이 optimal solution이 아닐 가능성이 크다고 한다. 하지만 identity mapping으로 가정하는 것이 자그마한 변화를 감지하기에 유리하다고 주장한다. 자그마한 변화는 F(x)를 뜻하고 F(x)는 F(x) + x = x를 최적화하는 과정에서 0에 가까운 값을 갖도록 학습이 되기 때문에 변화는 아주 미세하게 나타난다. 미세하게 변화되는 값을 처음부터 학습을 통해 찾는 것보다 애초에 0에 가까운 값을 갖도록 유도하는 것이 훨씬 쉽기 때문에 자그마한 변화를 감지하기 유리하다는 것이다.
그렇다면 자그마한 변화를 감지하는 것이 성능 향상에 있어 왜 이점이 있는 것일까? 아쉽게도 이 부분에 대해서는 본 논문에서 명쾌하게 답을 주지 않는다. 뇌피셜로 끄적여 본다면 일단 CNN 구조에서는 초기 층에서는 단순한 특성들이 추출되고 층이 깊어질수록 추상적인 형태의 특성들이 추출되게 된다. 하지만 층이 너무 깊어지게 되면 특성맵의 형태가 너무 추상화된 나머지 기존의 이미지의 특성을 제대로 추출하지 못하게 되고 이런 것들이 성능저하를 일으키는게 아닐까 싶다. 따라서 깊은 네트워크일수록 특성맵이 이전 layer에서의 형태와 차이가 크지 않도록 미세하게 변화를 주어 깊은 층으로 가도 성능 개선에 도움이 될 정도만큼의 추상화된 특징들을 뽑아낼 수 있도록 하는 것이라는 생각이다. Idnetity mapping의 중요성은 "Identity Mappings in Deep Residual Networks"라는 후속 논문에서 자세히 다뤄지는데 이 논문은 나중에 리뷰해보도록 하겠다.
3.2 Identity Mapping by Shortcuts

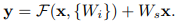
Residual block은 수식으로 다음과 같이 정의된다. 출력값 y는 잔차함수 F를 거쳐 나온 값에 shortcut connection인 x가 더해진 것이다. 이때 주의해야할 점은 위의 연산은 행렬 연산이라는 것이다. 따라서 conv layer를 통과하고 나온 행렬 F와 입력값인 행렬 x의 차원이 같아야 한다. 만약 둘의 차원이 다를 경우 projection 과정을 통해 차원을 맞춰줄 수 있다. 이때 적용된 shortcut을 projection shortcut이라고 한다. F와 x의 차원이 같아 shortcut이 그대로 적용되는 것을 identity shortcut이라 한다. 이후 서술될 실험에서 identity shortcut과 projection shortcut의 성능 차이는 별로 없으므로 연산량이 더 많은 projection은 shortcut connection에서 잘 쓰이지 않는다.
3.3 Network Architectures
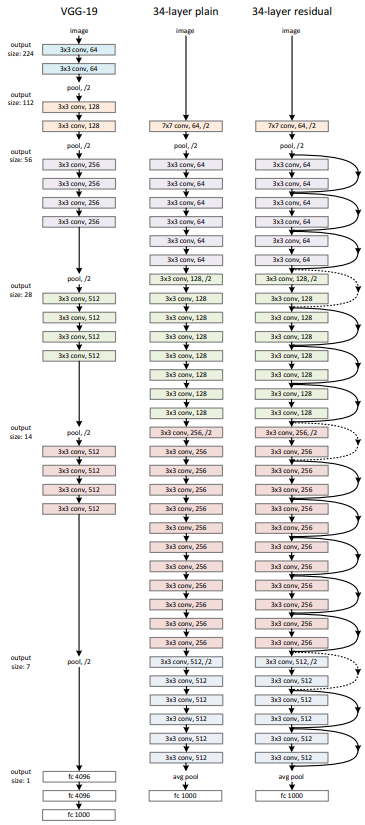
resnet은 VGG의 기본구조를 토대로 설계되었고 대부분의 합성곱 층이 3x3 filter를 사용하며 다음 두 규칙을 따른다.
1. 출력값의 특성맵 크기가 같은 층들에 대하여 같은 수의 filter를 사용한다.
2. 특성맵의 크기가 절반이 되면 각 층별 시간복잡도를 보존하기 위해 fiter의 수는 2배가 된다
donwsampling은 stride=2인 합성곱 층을 통해 수행되고 네트워크의 마지막에는 global average pooling, softmax가 적용되는 노드 1000개인 FC layer가 사용된다. 이러한 기본 구조를 토대로 다음 residual block으로 넘어가는 부분에 shortcut connections를 추가하는데 위 그림에서 점선으로 된 부분은 이 작업을 의미한다. 이때 shortcut connections은 intput과 output의 차원이 동일해야 적용이 가능하기 때문에 두 차원을 맞춰주는 작업이 필요한데 그 방식에 따라 zero-padding shortcuts, projection shortcuts두 방식으로 나뉜다.

이때 헷갈리지 말아야 할 점은 zero-padding이나 projection shortcut은 residual block을 첫번째로 돌 때 적용된다는 것이다. 위 그림의 34-layer을 보면 conv2_x에서 conv3_x으로 넘어올 때 처음에 conv3_x에는 28x28x64의 특성맵이 입력된다. conv3_x를 한차례 통과하고 나서의 출력값은 28x28x128이다. 따라서 shortcut connection을 진행하기 위해서는 zero-padding이나 projection shortcut을 적용해 두 특성맵의 차원을 맞춰주는 과정이 필요하다. 이 과정을 한번 진행하고 나면 conv3_x를 다시 돌 때는 입력값이 28x28x128이 되기 때문에 identity shortcut을 적용할 수 있다. 그렇게 총 4번 residual block을 도는 과정에서 처음을 제외한 나머지 3번동안 identity shortcut이 적용되는 것이다. 물론 이 때에도 projection shortcut을 사용할 수 있겠지만 굳이? 이다. 한번 아래의 표를 봐보자.

위 표에서 A는 차원을 맞춰줄 때 zero-padding shortcut, B는 차원을 맞춰줄 때 projection shortcut, 다른 부분에서는 identity shortcut, C는 모든 부분에 projection shortcut을 사용하여 성능을 책정한 것이다. A는 성능이 B, C에 비해 상대적으로 낮은데 이는 A에서는 잔차학습이 이루어지지 않기 때문이라고 한다. B와 C는 성능이 비슷하지만 C에서 파라미터가 더 많아 훨씬 더 복잡한 계산이 요구되기 때문에 C는 이 논문에서 사용되지 않았다. 애초에 입력값과 출력값의 차원이 동일한 상황에서는 그냥 입력값을 그대로 가져와 쓰면(identity shortcut) shortcut connection을 진행할 수 있기 때문에 연산량만 늘리는 projection shortcut을 굳이 쓸 필요가 없다는 것이다.
Bottleneck 구조와 1x1 convolution
이 논문은 계산 시간과 복잡도의 개선을 위해 bottleneck 구조를 제안한다. 이는 기존에 하나의 building block에서 2개의 합성곱 층을 사용한 것과 다르게 1x1, 3x3, 1x1 순서로 3개의 합성곱 층을 사용한다.
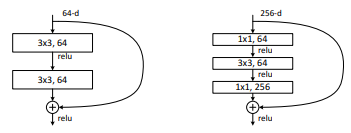
오른쪽 bottleneck 구조를 보면 shortcut connection은 identity connection을 적용하고 building block의 합성곱 층들에서1x1 convolution을 통해 projection 과정이 진행되는 것을 알 수 있다. shortcut connection에서 identity connection을 사용하면 추가적인 연산 없이 입력값만 가져오면 되기 때문에 연산을 줄이는데 이점이 있다는 것이 직관적으로 와닿지만 1x1 convolution은 어떤 이점이 있는 것일까?
1x1 convolution은 1x1 filter의 개수만큼 특성맵을 생성해 낸다. 즉 28x28x256의 특성맵에 1x1x32의 특성맵을 적용하면 28x28x32의 특성맵이 생성되는 것이다. 만약 28x28x256의 특성맵에 3x3x64의 filter를 적용시킨다고 하면 필요한 파라미터 수는 115.6M개이다. 하지만 28x28x256의 특성맵을 1x1x32의 필터를 적용시켜 28x28x32로 크기를 줄이고 그 이후에 3x3x64를 적용시킨다면 6M+14.4M = 20.4M개의 파라미터만 있으면 된다. 확실히 1x1 convolution을 사용하면 계산량이 훠어어어얼씬 줄어들게 된다. 1x1 convolution가 서로다른 두 차원을 동일하게 맞춰주는 방식과 그 이점에 관해서는 아래 링크에서 아주 깔쌈하게 설명을 잘 해놨기 때문에 참고 바란다.
shotout to
https://hwiyong.tistory.com/45
1x1 convolution이란,
GoogLeNet 즉, 구글에서 발표한 Inception 계통의 Network에서는 1x1 Convolution을 통해 유의미하게 연산량을 줄였습니다. 그리고 이후 Xception, Squeeze, Mobile 등 다양한 모델에서도 연산량 감소를 위해 이 방
hwiyong.tistory.com
4. Experiments
4.1 ImageNet Classification
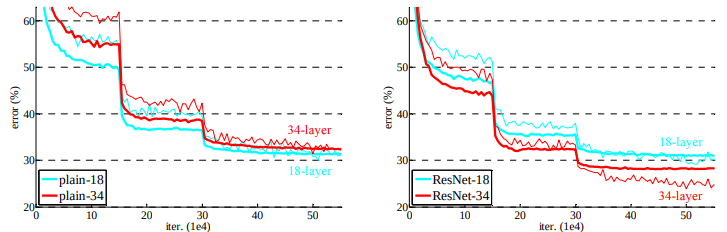
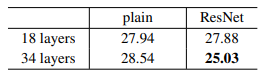
다음은 resnet 모델을 실험을 통해 비교해놓은 파트이다. plain networks에서는 더 깊은 네트워크의 오류가 높은데 18, 34층의 네트워크 모두에서 배치정규화가 적용되기 때문에 이는 기울기 소실의 문제로 보기는 어렵다. 본 논문에서는 깊은 네트워크에서 수렴률이 매우 낮아서 오류가 더 높게 나오는 것으로 추측하고 있다. residual networks에서는 모든 shortcuts에 대하여 identity mapping이 적용되고 차원을 늘리는데에(다음 residual block으로 넘어갈 때) zero-padding shortcut이 적용되었는데 얕은 층보다 더 나은 성능을 보였고 degradation 문제는 확실히 줄어든 모습을 보인다. 그런데 18 layer의 pain, resnet error를 보면 별로 차이가 없지만 resnet에서 수렴이 더 빠르다.(라고 논문에서 말하지만 내 눈에는수렴 속도엔 차이가 없어보이는디?) 이는 resnet이 최적화를 용이하게 해 수렴이 더 빨리 되는 것이라고 한다.

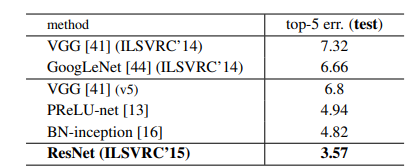
50층 이상의 resnet 구조에서부터는 bottleneck 구조가 적용된다. 이러한 구조를 활용한 resnet은 놀랍게도 152층으로 아주 깊게 쌓은 층도 효과적인 성능을 나타내고 있음을 확인할 수 있다. 서로 다른 깊이의 resnet을 앙상블 하면 성능은 더욱 개선된다. 그리고 이 앙상블 모델이 2015 ILSVRC에서 우승을 차지했다.