분류모델 평가지표: confusion matrix, accuracy, precision, sensitivity(recall), specificity, F1, ROC curve & PR curve(AUC, AP, mAP)

 

 

머신러닝/딥러닝을 공부하다보면 아주 다양한 모델 평가지표들을 볼 수 있다. confusion matrix(혼동행렬)은 분류 모델의 평가지표의 뼈대를 이룬다고 할 수 있는데 confusion matrix의 여러 값들을 조합하여 다양한 평가지표를 구성하게 된다. 

confusion matrix

 

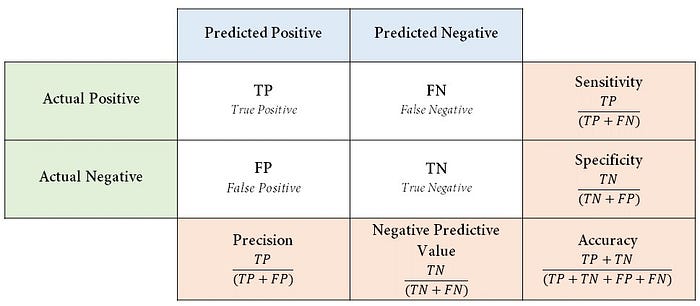
혼동행렬은 실제 범주를 어떻게 예측했냐에 따라 다음과 같이 네 가지로 상황이 나뉜다.

True positive(TP): 실제 참인 값을 참이라 예측(오류)
False positive(FP): 실제 거짓인 값을 참이라 예측
False negative(FN): 실제 참인 값을 거짓이라 예측
True negative(TN): 실제 거짓인 값을 거짓이라 예측(오류)

 

그리고 이 값들로 적절한 수식을 만들어 분류모델의 평가지표를 구할 수 있다. 평가지표로는 정밀도(Precision), 민감도(Sensitivity) 특이도(Specificity), 정확도(Accuracy)가 있다. 하나씩 차근차근 알아가보자.

* 아래 설명은 위의 혼동행렬 표를 참고해가며 읽어보도록 하자

 

 

① 정밀도(Precision)

 

$\displaystyle\frac{TP}{TP+FP}$

 

정밀도는 긍정으로 예측했을 때 들어맞은 예측의 비율을 계산하는 지표다. 정밀도가 높다는 것은 긍정적인 예측이 적중할 확률이 높다는 것을 의미하고 이는 곧 데이터의 분산이 낮음을 의미한다. 실제 범주가 1인 데이터를 1로 예측한 비율이 많아지면 실제, 예측치의 차이의 정도를 나타내는 분산이 낮아지는 것은 자연스럽다. 따라서 높은 정밀도를 보이는 데이터는 안정성이 높은 데이터로 간주될 수 있다. 하지만 정밀도는 예측 값이 긍정적일 경우에 대한 정보만 나타내기 때문에 해당 모델이 부정적인 값들을 예측한 경우에 대해 그 결과를 얼마나 신뢰해야 하는지는 알 수 없다. 정밀도는 후술할 F1 지표를 나타내는데 사용된다.

정밀도가 평가지표로 사용되는 예시로 스팸메일 분류기가 있다. 스팸메일 분류기에서는 중요한 메일을 스팸이라 판별하면 문제가 심각해진다. 따라서 스팸메일이라 판별한 것(Positive) 중에서 중요 메일(Negative)의 비율(FP)을 낮추는 것이 핵심이다. 정밀도는 FP가 낮아질수록 더 높아지므로 스팸메일 분류기의 성능을 잘 나타낼 수 있다.

 

 

② 민감도(Sensitivity) = 재현율(Recall)

 

$\displaystyle\frac{TP}{TP+FN}$

 

민감도(=재현율)은 실제값이 긍정인 경우들 중에서 긍정의 예측값을 도출할 비율을 나타내는 지표이며 TPR(True Positive Rate)라고도 한다. '재현율'이라는 워딩에 대해 생각해보면 이는 실제 긍정의 값들을 모델이 얼만큼 긍정으로 재현해 낼 수 있는지에 대한 정보를 제공하는 지표임을 알 수 있다. 긍정의 결과에 민감에게 반응하는 정도로 이해하면 '민감도'라는 말이 와닿을 것이다. 민감도는 현실이 긍정인 경우들만 고려하기 때문에 현실이 부정일때의 예측에 관한 정보는 알 수 없다. 재현율 또한 F1 지표를 나타내는 데 사용되고 ROC 곡선을 산출하는 데에도 쓰인다. 1 - sensitivity를 계산하면 실제값 긍정일 때 부정으로 예측할 확률인 FNR(False Negative Rate)을 구할 수 있다.

민감도가 평가지표로 사용되는 예시로는 암 판별기가 있다. 암 판별기에서는 실제 암인데 암이 아니라 판별하면 문제가 심각해진다. 따라서 암이 아니라 판별한 것(Negative) 중에서 실제 암(Positive)인 비율(FN)을 낮추는 것이 핵심이다. 민감도는 FN이 낮아질수록 더 높아지므로 암 판별기의 성능을 잘 나타낼 수 있다. 

 

민감도(재현율)과 정밀도의 trade-off 관계
민감도와 정밀도의 trade-off 관계란 민감도와 정밀도는 서로 반대로 움직인다는 것이다. 민감도가 높아지면 정밀도는 낮아지고 정밀도가 높아지면 반대로 민감도가 낮아진다. 그럼 왜 그렇게 되는 것일까?
일반적으로 이진분류의 상황에서는 Positive와 Negative로 구분하는 임계값(threshold)가 존재한다. 임계값을 낮추게 되면 모델이 Positive로 예측하는 횟수가 많아지고 Negative로 예측하는 횟수는 적어진다. Negative 예측 수가 줄어드니 당연히 FN(실제 Positive, 예측 Negative)값은 낮아지고 민감도는 커지게 된다. Positive 예측 수가 늘어나면 거짓 Positive(FP)가 늘어날 수 밖에 없다. 따라서 정밀도는 낮아지게 되는 것이다.

 

 

③ 특이도(Specificty)

 

$\displaystyle\frac{TN}{TN+FP}$

 

특이도는 실제값이 부정인 경우들 중에서 부정의 예측값을 도출할 비율을 나타내는 지표이며 TNR(True Negative Rate)라고도 한다. 이는 민감도와는 반대로 실제값이 긍정인 경우에 대한 정보를 알 수 없다. 1 - spectificity를 계산하면 실제값이 부정일 때 긍정으로 예측할 확률인 FPR(False Positive Rate)을 구할 수 있다. FPR(= 1 - specificity)는 ROC curve의 x값으로 활용된다. 

 

 

④ 정확도(Accuracy)

 

$\displaystyle\frac{TP+TN}{TP+TN+FP+FN}$

 

confusion metrix in balanced data

confusion metrix in imbalanced data

 

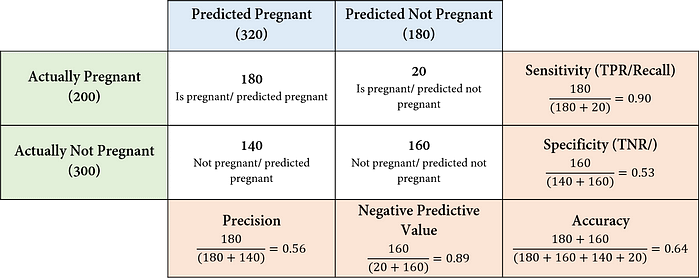
정확도는 전체 예측 중에서 들어맞은 예측의 비율을 계산하는 지표다. 정확도는 균형 데이터에서는 좋은 성능 지표가 된다. 위쪽 표의 균형 데이터에서 정밀도를 평가지표로 활용하면 0.56으로 썩 좋은 모델은 아니지만 민감도를 평가지표로 활용하면 0.90으로 꽤나 좋은 성능을 내는 모델이 된다. 애초에 threshold를 낮춰 Positive로 비교적 많은 예측을 때려버린 모델이라 정밀도는 낮아지고 민감도는 커지게 되기 때문에 이 둘을 성능지표로 활용하는 것은 별로 좋은 생각이 아니다. 이때 정확도가 효과적인 것이다. 정확도는 confusion matrix의 모든 값들을 활용해 지표를 계산하므로 민감도와 정밀도에 비해 꽤나 중립적인 값을 도출한다. 

 

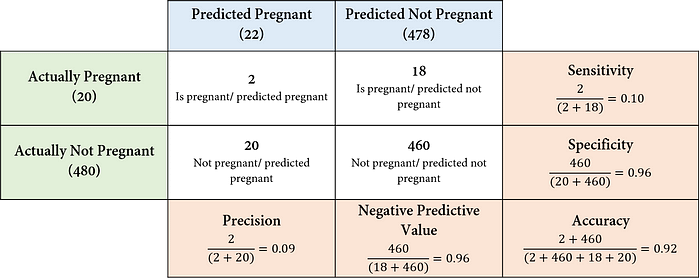
하지만 아래쪽 표의 불균형 데이터를 보면 모델은 20개의 Positive중에 2개밖에 제대로 예측하지 못하고 있는데 정확도는 92%이다. 위 데이터에서는 Positive를 정확하게 예측하는 것이 중요한데 이를 하나도 예측하지 못한다 하더라도 정확도가 90%가 넘는다. 본 데이터에서는 정확도는 전혀 쓸모가 없는 것이다. 따라서 Positive class의 예측값과 실제값을 잘 반영하는 정밀도와 민감도를 사용하는 것이 적절하다. 하지만 정밀도와 민감도를 사용할 때에도 문제가 있다. 만약 모델이 모든 경우를 Pregnant라고 예측한다면 민감도는 1이 되지만 정밀도는 최대 0.04이다. 민감도를 평가지표로 쓰면 아주 완벽한 모델이 되지만 실제로 모든 경우를 Positive로 예측하는 모델은 형편없는 모델이다. 차라리 정밀도가 모델의 성능을 제대로 나타낸다고 할 수 있다. 그렇다고 무턱대고 정밀도를 쓰면 문제인게 임신 판단에 있어서는 FN를 줄이는 것이 중요하지만 정밀도는 이에 대한 고려가 전혀 없기 때문이다.  따라서 민감도와 정밀도를 적절히 고려할 수 있는 지표가 필요하다. 그 대표적인 예가 F-Measures이다.

 

⑤ F- Measures

 

F1 score

$ F1 = \displaystyle\frac{2*Precision*Recall}{Precision+Recall}$

 

F1은 정밀도와 민감도의 조화평균으로 둘 사이의 중간값을 나타낸다. 일반적으로 조화평균은 더 적은 값에 영향을 많이 받기 때문에 정밀도와 민감도 중 더 작은 값에 치우쳐진 상태로 값이 나온다. 이때 F1은 단순히 정밀도와 민감도의 조화평균이므로 FN과 FP가 동등하게 중요한 데이터의 모델 성능지표로 적합하다. 

 

F2 score

$ F2 = 5*\displaystyle\frac{Precision*Recall}{4*Precision+Recall}$

 

F2의 식을 보면 F1과 같이 그냥 조화평균을 낸 것은 아니라는 것을 알 수 있다. 정밀도의 값을 4배 시킨 뒤 조화평균을 낸 후 그 값에 5/8을 곱해주면 F2 score가 나온다. 이렇게 되면 F2의 값은 재현율(민감도)에 더 가까운 값을 도출하게 된다. 만약 정밀도가 0.1, 재현율이 0.8이라면 이 둘을 그냥 조화평균을 내기 보다 정밀도를 0.4로 키워준 뒤 조화평균을 내는 것이 재현율에 값을 더 근접하게 도출시킬 수 있는 것은 당연하다. 이는 곧 재현율에 더 가중치를 두어 평가지표를 도출하는 것이라 할 수 있다. 앞서 말한 암 판별기와 같이 예측한 양성이 틀리더라도 실제 양성을 하나라도 더 분류해내고자 할 때(FN↓ 중요한 경우) F2를 사용한다. 

 

F0.5 score

$ F0.5 = \displaystyle\frac{4}{5}*\frac{Precision*Recall}{0.5^{2}*Precision+Recall}$

 

반대로 F0.5는 정밀도에 더 작게 만드는 작업이 들어간다. 따라서 이는 정밀도에 더 가깝게 값을 도출하는 즉 정밀도에 더 가중치를 두는 평가지표라고 할 수 있다. F0.5는 FP를 낮추는 것이 더 중요할 때 사용되는 지표이기 때문에 스팸메일 분류기와 같은 모델에 사용하는 것이 유리한 지표라 할 수 있다. 

 

이와 같이 F 뒤에 오는 숫자에 따라 정밀도와 민감도 중 어느 곳에 더 가중치를 둘지 조정할 수 있는데 이를 일반화된 식으로 표현하면 다음과 같이 된다. 이를 F-베타 score 라고 한다.

 

$F_{\beta} = \displaystyle(1+\beta^2)\cdot\frac{Precision\times Recall}{(\beta^2\times Precision)+Recall}$

 

⑥ ROC-curve(AUC) & PR-curve(AP)

ROC curve와 PR curve는 다양한 임계값(threshold)에서 모델의 성능을 나타내는 그래프이다. ROC curve는 x축에 1-특이도(FPR) y축에 민감도(TPR)을 PR은 x축에 민감도(재현율)을 사용하여 모든 임계값에서의 각각의 수치를 그래프로 표현하였다. 이는 모델이 양성으로 판단한 것이 맞는지와 틀린지 모두 고려한다고 할 수 있다. 즉 모델의 정확성과 오류를 동시에 고려해 표현하는 것이다. PR curve는 x축에 재현율(민감도), y축에 정밀도를 사용해 모든 임계값에서 각각의 수치를 표현한 그래프이다. 이렇게 나온 ROC와 PR 그래프의 아래 면적을 계산한 값을 AUC라고 하고 각각을 AUROC, AUPRC라 할 수 있다. F score와의 차이점으로는 F score는 여러 임계값에 따른 모델의 성능을 한번에 표현하지는 못하지만 ROC와 PR은 AUC를 통해 이를 실현한다. 

 

위의 그림은 임계값의 변화에 따라 ROC curve와 PR curve가 그려지는 과정을 나타낸 것이다. 임계값이 올라갈수록 FP(파란x)는 TN(파란점)으로 바뀌며 FPR은 점차 줄어든다. 임계값이 어느정도 이상에서는 TP(주황점)이 FN(주황x)으로 바뀌게 되고 민감도(재현율) 또한 점차 줄어든다. 임계값이 커질수록 예측 양성 중 TP의 비율은 증가하는데 이에 따라 정밀도는 점차 커진다. 이를 그래프로 표현한 것이 ROC curve, PR curve인 것이다.

 

ROC를 사용하면 (1)임계값에 따른 모델의 TPR과 FPR을 한번에 확인할 수 있고 (2)임계값을 어디로 잡을지에 대한 판단을 하기 쉬우며 AUC를 통해 (3)모든 임계값에 따른 모델의 정확성과 오류를 종합적으로 고려한 성능지표를 도출해낼 수 있다. 이렇게 보면 ROC가 상당히 괜찮은 지표인데 PR은 왜 사용하는 것인지 의문이 들 것이다.

 

ROC curve and PR curve in imbalanced data

 

그것은 바로 ROC가 음성이 아주 많은 불균형 데이터에 취약하기 때문이다. 위의 그림을 한번 보자. 왼쪽 그림을 보면 데이터의 음성 비율이 아주 많지만 음성과 양성 class의 prediction score가 겹치는 부분이 아주 많다. 모델이 음성과 양성을 제대로 분리하지 못하고 있는 것이다. 임계값이 낮아질수록 실제 양성을 양성이라 판별을 잘 하게 되지만 그만큼 아주 많은 음성의 데이터들에도 그냥 양성이라고 판정을 때려버리게 된다. 위의 그림에서 양성의 데이터와 음성의 데이터가 겹쳐있는 부분에서 대부분의 양성 데이터가 분포하고 있지만 음성은 겹치지 않는 아래부분에 데이터가 훨씬 더 집중적으로 분포돼있다. 따라서 임계점이 낮아질 때 FPR은 조금씩 증가하는 반면 TPR(민감도)는 급격하게 증가한다. 따라서 음성과 양성을 판단하는 지점이 겹쳐있을수록 모델의 성능은 더 떨어짐에도 불구하고 ROC curve는 그 부분을 포착해내기 어렵게 된다. 이때 PR curve를 사용하면 이러한 문제를 해결할 수 있다!

PR curve는 y축으로 정밀도를 사용한다. 정밀도는 분모가 예측 양성이고 분자가 예측양성중 실제 양성이다. 음성의 비율이 아주 많은 위와 같은 데이터에서 좋지 않은 모델은 임계값이 낮아질수록 그  많은 음성들을 양성으로 예측해버리기 때문에 분모(예측 양성)는 많이 커진다. 하지만 실제 양성 데이터 자체는 매우 적기 때문에 분자(예측양성 중 실제양성)은 조금밖에 커지지 않는다. 따라서 y 값인 정밀도가 급격히 낮아질 수 밖에 없다. 즉 모델이 음성과 양성을 제대로 분리하지 못하는 것을 ROC는 놓쳤던 반면 PR은 '정밀도' 덕분에 포착할 수 있는 것이다. 그 결과 ROC-AUC로는 꽤나 좋은 성능을 내는 것으로 평가받던 모델의 실상이 PR-AUC를 통해 적나라하게 드러나는 것을 확인할 수 있다. 이러한 PR curve는 이상탐지 같이 양성의 데이터가 희박한 분야에서 활용하면 아~주 유용하다. 

 

⑦ AP & mAP

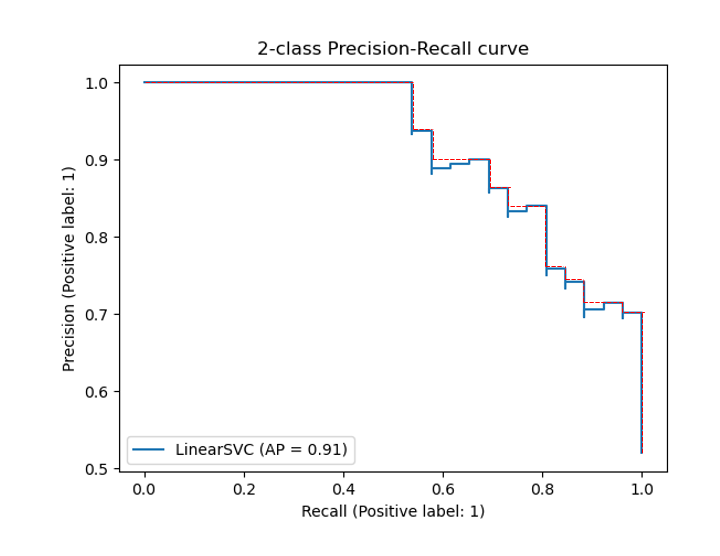
AP는 그래프 아래의 넓이를 구한다는점에서 AUROC와 유사하지만 조금 다른 점이 있다. AP는 위 그래프와 같이 PR곡선이 단조적으로 감속하는 그래프가 되도록 수정한 후 그 아래 면적을 구하는 방식으로 산출된다는 것이다. 그렇다면 왜 이러한 변환을 시켜주는 것일까? 그 이유는 위의 불균형한 데이터셋의 그림을 보면 알 수 있다. 임계값이 맨 위에서 내려올 때 처음에는 양성 1개가 양성으로 예측되기 때문에 precision은 1이다. 조금 더 내려오면 양성1개 음성1개가 둘다 양성으로 예측되므로 precision은 0.5가 된다. 그다음 더 내려오면 양성2개 음성1개가 양성으로 예측되므로 precision은 0.66이 된다. 보면 precision의 값은 실제 음성이 양성으로 예측될수록 낮아진다. 그 결과 precision의 값은 계속 요동치게 되고 모델이 양성을 제대로 판별하는지 평가하는데에 지장을 준다. 따라서 좀 더 정확한 평가지표의 구성을 위해 음성 데이터의 영향을 제거한 것이 AP인 것이다. 

 

일반적으로 객체 탐지 모델은 탐지하고자 하는 객체(class)가 강아지, 고양이, 사람 등등 다양하다. 이에 따라 각 객체별 AP의 평균인 mAP가 평가지표로 사용되는 것이다.

 

 

 

 

 

 

 

 

 

 

 

https://github.com/rafaelpadilla/Object-Detection-Metrics?tab=readme-ov-file#precision-x-recall-curve

GitHub - rafaelpadilla/Object-Detection-Metrics: Most popular metrics used to evaluate object detection algorithms.

 

 

참고자료

 

https://namu.wiki/w/%ED%98%BC%EB%8F%99%ED%96%89%EB%A0%AC#s-2.2

혼동행렬

 

https://medium.com/@danyal.wainstein1/understanding-the-confusion-matrix-b9bc45ba2679

Understanding the Confusion Matrix

 

https://techblog-history-younghunjo1.tistory.com/101

[ML] Precision 과 Recall의 Trade-off, 그리고 ROC Curve

 

https://velog.io/@kwjinwoo/mAP

mAP(mean average precision)

 

https://rfriend.tistory.com/774

[Python] 불균형 데이터에 대한 분류 모델 성과평가 지표 (performance metrics of binary classification for imbal

 

 

https://towardsdatascience.com/on-roc-and-precision-recall-curves-c23e9b63820c

On ROC and Precision-Recall curves